+Introduction - Working with sets of data

At the heart of any Grasshopper definition is the data. Grasshopper components process and create data, while wires transport the data between different components. In the last exercise, you may have already noticed that some wires look different from each other. This is because the visualization of the wire changes based on the structure of the data flowing through it. There are three types of data that can flow through a wire in Grasshopper:

• Item: one data element, for example one curve object
• List: an ordered set of elements, for example 10 points
• DataTree: a more complex data structure composed of two or more Lists

DataTrees are the subject of the next section. For now, let's focus on Lists, and how to work with them in Grasshopper.

+Lists

+Creating lists

Many components generate Lists of items as a result of their operation. For example, the Divide Curve component we saw in the first exercise uses one curve and a value specifying the number of divisions to create a List of points along the Curve.

To create your own List from scratch, you can input multiple values into a Panel component. A shortcut for creating a Panel is to double-click on the canvas to bring up the search bar, then type '//'. This will create a new Panel, and place any text you type after the two slashes into the Panel. A Panel can be used to input text or numerical data. To create a List of values, put them on separate lines in the Panel. Make sure to right-click on the Panel and select the option for 'Multiline Data' to separate the lines into different items in a list. Otherwise, the text will be output as one big chunk.

You can find many useful components for creating and manipulating Lists in the 'Sets' tab in Grasshopper's component toolbar.

The 'Sets' tab of the component toolbar contains many useful tools for working with Lists

In the 'Sequence' section of the 'Sets' tab, you will find several components for generating sets of numbers, which can be very useful for driving your computational models. In the previous exercise we used the Series component to generate a set of numbers given a starting value, a step value between each number, and a total number of values to generate.

The Range component also generates a set of evenly spaced numbers, but it does so based on a Domain that defines the minimum and maximum value, and the total number of values to generate within that range.

The Random component will also generate a set of values within a given Domain, but it will choose the values randomly. To create different sets of random values, you can input different numbers into the Seed (S) input, which controls how the random algorithm is run. While the numbers created by the Random component will always appear random, inputting the same Seed will always produce the same set of numbers. This is important for making sure that the numbers don't change each time you re-run the script.

+Seeing the data

A quick way to see the data stored inside a component is to hover over any of the component's input or output ports. A tooltip will pop up with a preview of the data stored inside the port. You can also pass the data into the input port of a Panel component, which will display the data in a scrollable table. This is a great way to monitor the data being produced by your definition and keep it visible on the canvas.

In the table generated within the Panel, you will notice that each value in the List has a corresponding number to the left of it. This is the index of the item, and it represents the item's position in the list. You will also notice that the first item's index is 0, not 1 as you might expect. This is because in Grasshopper, as in most programming languages, elements are numbered starting with 0. This can take some getting used to but you will get the hang of it over time.

+Working with Lists

In the 'List' section of the 'Sets' tab, you will find many useful components for manipulating Lists, including:

• The List Length component which returns the length of a list
• The List Item component which returns a List item at a specified index
• The Sort List component which sorts the items in a List
• The Reverse List component which reverses the order of a List

Spend some time exploring these components on your own, we will see some of them again in later exercises.

+Working with Domains

A Domain is a special data type in Grasshopper that represents a numerical range based on a start and end value. Domains are used by many components that operate over a range of values. We've already seen how Domains are used by the Range and Random components to generate sets of numbers.

The easiest way to create a Domain is to type it into a Panel component with the starting and ending value separated by ' to ', for example: '0 to 100'. If you pass this text into an input that expects a Domain, Grasshopper will automatically convert it for you. If you want more control over how the Domain is defined, or want to control the start and end values using data in your definition, you can use the Construct Domain component which creates a Domain from two input values.

The Construct Domain component can be found in the 'Domain' section of the 'Maths' tab in the component toolbar. Here you will find several other useful tools for working with Domains.

The Remap Numbers component maps a set of numbers from one Domain to another. For example, you can use the Remap Numbers component to take data in the range of [0, 100] and map it to a range of [0.0, 1.0]. The Remap Numbers component has three inputs: the data (D) you want to map, the starting domain (S) representing the range of the current data, and the target domain (T) representing the range you want to map the data to.

A very common application of the Remap Numbers component is mapping a List of values to a Domain of 0.0—1.0 so that the lowest value in the List becomes 0.0 and the highest value becomes 1.0. To find the starting Domain of the data we can use the Bounds component which returns a Domain defined by the smallest and largest values in a List. We can use the output of the Bounds component as the starting Domain (S) of the Remap Numbers component to map the values to the default target Domain of 0.0-1.0.

Combining the Bounds and Remap Numbers components to map a List of values to the range 0.0-1.0

+How Lists affect the data flow

Each component in Grasshopper defines a process for taking in a set of inputs and producing a set of outputs. Most components are built to work with single items as inputs. For example, the Line component creates a line using one start point (A) and one end point (B) as inputs.

The Line component generating a single line given two individual points

When we pass a List of values into a component's input port instead of a single item, the component will actually run multiple times, as many times as it needs to process each item in the List in order. For example, if we pass ten points into the Line component's (B) input, the component will actually run ten times and produce ten lines as a result, with each resulting line using one of the ten provided end points. Since we only supplied one start point, the same point is used for each line.

Multiple lines produced based on a List of points

Now, what happens when we pass multiple points into the other input as well? In this case, Grasshopper will go down both lists at once, using one point from each list in order to create each line. You can see that the component stills runs ten times to produce ten lines, but this time each line has a unique start point.

Multiple lines produced based on two Lists of points

If you input Lists of different lengths into the same component, the component will still run as many times as it needs to in order to process all the items in the longest List. For the shorter List, the component will use as many unique items as possible until it runs out of items, and then reuse the last item until all values in the longest List are used up. For example, if we only pass six points into the Line component's (A) input, the component will still run ten times, but the last five lines will share the same start point.

+Working with data

So far, we have seen how Grasshopper uses Lists to store data containing multiple items. Working with Lists and predicting how the structure of your data will impact the way a component will run can be challenging when you're first learning Grasshopper. It can even be challenging for those used to programming with a text-based programming language, where processes for creating and working with data can be described much more explicitly.

What you need to remember is that everything in Grasshopper is defined by individual components that execute specific functions and generate new data based on the data given to them. Thus, unlike traditional code, a Grasshopper definition is not so much a set of instructions as a complex system for developing formal solutions based on a set of interrelated parts. Learning to control the data in our definitions and getting an intuition for how the data structure will impact various components is a critical part of becoming an expert in Grasshopper, and like everything else, it is best learned through practice.

Let's continue our discussion of working with data in Grasshopper by looking at DataTrees, which define more complex data structures composed of two or more individual Lists.

+DataTrees

+What are DataTrees?

In Grasshopper, DataTrees are used to organize data in more complex structures than a single ordered List. An easy way to think of DataTrees is as a collection of Lists. If a List is a structure for organizing two or more items of data, a DataTree is a structure for organizing two or more Lists.

Each List in a DataTree is called a branch. Just as every item in a List has an index that specifies its position in the List, each branch in a DataTree has a path that specifies its location in the DataTree. Thus, any item in a DataTree can be retrieved by specifying the path of the branch the item is on, followed by the index of the item in that branch.

DataTrees use a hierarchical structure to organize their branches, which is reflected in the structure of its branch paths. For example, let's take a DataTree composed of four branches. In one case the DataTree might have one level of hierarchy with each branch organized on the same level. In this case, each branch would have a path composed of a single number to specify its position on that level. In another case, we might want to organize the branches in two levels of hierarchy with two groups of two branches. In this case, the branches would have paths composed of two numbers, each number specifying the position of the branch at each level of the hierarchy.

Example of two DataTrees with different hierarchies for organizing four branches

DataTrees are often created when a component that produces a List of data from a single input value is supplied a List of input values. For example, the Divide Curve component we saw in the first exercise takes a single Curve and produces a List of points as a result. If we input a List of Curves instead, the result will be a DataTree, with the List of points resulting from dividing each Curve represented as individual branches in the tree. The heirarchy of branches in a DataTree often reflects the history of how the data was produced as it was passed between different components in the definition.

Extending the first exercise to create a DataTree of circles organized hierarchically into branches

+Visualizing DataTrees

When you first start working with DataTrees, it can be difficult to keep track of the structure of the data being produced. Often it helps to visualize the data to understand not only what it is but how it's structured into branches and the hierarchy of that structure.

There are three basic ways to visualize the structure of a DataTree. The first two we've already seen above:

Hovering over any input or output port will give you a tooltip with a preview of the data. If that data is in a DataTree format, however, you will not see the actual data items but a list of the branches with their paths and the number of items in each branch.

You can also pass the data into a Panel component, which will show each element in the DataTree organized by branch. Each branch is denoted by a dark bar with the path of that branch in it.

Finally, there is also a special component for visualizing the branch structure and hierarchy of a DataTree called Param Viewer. This component has two modes for visualizing DataTrees which you can switch between by double-clicking on the component.

The first mode will list the branches in a DataTree, showing the path of each branch and the number of elements in each (this is similar to the tooltip display you get from hovering over an input or output port). The second mode gives you a visual representation of the DataTree showing the levels of hierarchy and path of each branch.

+Working with DataTrees

The 'Tree' section of the 'Sets' tab in the component toolbar has many useful components for working with DataTrees.

• Flatten Tree: removes all branch hierarchy and moves all elements to a single branch. In effect, it converts a DataTree into a List.

• Graft Tree: adds a level of hierarchy to a DataTree by placing all the items in every branch onto their own branches. Passing a List into a Graft Tree component creates a DataTree with a separate branch for each item in the List.

• Simplify Tree: simplifies the DataTree as much as possible by removing unnecessary levels of hierarchy. This can be useful for cleaning up overly complex DataTree structures that may have been created as the data was passed through multiple components.

• Explode Tree: breaks the branches of a DataTree into individual Lists represented by individual outputs in the component. This component has a zoomable UI which you can use to add outputs and specify the branch path the output should pull data from. To automatically match the outputs to the structure of the DataTree you can right-click on the component and select 'Match outputs' from the context menu.

Using the Explode Tree component to separate DataTree branches into individual Lists

• Flip Matrix: for DataTrees with only one level of hierarchy (all branches organized on the same level), this component flips the relationship between the paths of each branch and the index of the items in each branch. For example, if you input a DataTree composed of five branches with ten items in each branch, the Flip Matrix component would produce the same exact data but now organized as ten branches with five items in each branch. The first items of each branch would go into the first branch, the second items of each branch would go into the second branch, and so on. This is similar to transposing a table by flipping the rows and columns.

• Path mapper: allows you to change the structure of a DataTree by indicating the starting and ending path hierarchy. Right-clicking on the component will display a context menu where you can select from several common mapping types. A very useful one is 'Trim Mapping' which trims the furthest branches of a tree by combining elements with the same path one level below on a single branch. A good way to get familiar with what the Path Mapper component can do is to start with one of the presets and then double-click on the component to experiment with editing the mapping further.

Using the Path Mapper component to trim the branches of a tree

Some of the most common data manipulations such as Flattening and Grafting a DataTree or reversing the order of a List can be applied as a filter directly to data as it enters or leaves a component. To apply a filter, right-click on a component's input or output port and select it from the context menu. This is also a quick way to experiment with different data manipulations if you are trying to get your data to fit what a certain component needs.

Applying filters to modify the structure of a DataTree in a component's outputs

+How DataTrees affect the data flow

Earlier, we saw how inputting a List of data into a component that expects a single item causes the component to run multiple times, producing multiple outputs as a result. When you input two Lists into a component, the component will run as many times as it needs to process every item in both Lists, reusing items from the smaller Lists as necessary. When you input multiple DataTrees into a component, this same process is extended to the branches of the DataTrees.

The component will first match branches between the trees, and then for each pair of branches it will work through all the elements in both branches the same as it would for multiple Lists. If one DataTree has more branches than another, the last branch from the smaller DataTree is reused as necessary until all the data has been processed.

Let's look back at the previous example where we were connecting multiple lines using two lists of points. We saw that inputting two lists of ten points created ten lines, one line using each pair of points from both lists. But what if we wanted to generate 100 lines, with a line connecting each start point to each end point?

This is where DataTrees come in. To get each start point to be processed using each end point, we can use the Graft component (or filter) to convert one of the inputs from a List of ten points to a DataTree with ten branches, each one containing one point.

When the Line component gets the List and DataTree as inputs, it will first match the branches in each data set. In Grasshopper, DataTrees are not a separate concept from Lists, but an extension that allow you to work with multiple Lists within the same dataset. In fact, a List in Grasshopper is actually just a DataTree with a single branch. You will notice that when you view a List in a Panel, there is still a branch index at the top of the list with the default path {0;0}.

Thus, when the Line component is matching branches between the List and DataTree, it will use the same single branch of ten points to compare to each branch in the DataTree. The ten points in the List will be used to generate ten lines for the single point in each of the ten branches of the DataTree. The result is a DataTree containing ten branches, with ten lines on each branch, or 100 lines total.

Grafting a List to compare each element in one list to every element in another

+Exercise: Parametric facade

Managing DataTrees and using their structure to control how components function can be one of the hardest challenges when you're first learning Grasshopper. Because Grasshopper does not allow us to write explicit instructions for how the components should run, often the only way to get a component to do what you want it to do is to first structure the data you pass into it the right way. As we saw with the previous example, the same ten points passed through the same component can produce very different results depending on how those ten points are organized in the data.

Learning how to work with DataTrees effectively will take time, and like most things Grasshopper, the best way to learn is by doing. In the following exercise we will continue to develop our parametric tower model, this time focusing on creating a panelized facade system for the curving tower. In the digital world, there are few limitations on geometry, and modern CAD tools like Rhino and Grasshopper make it easy to model free-from curve geometries of high complexity. However, if the goal of the model is to design an object that will be made in the physical world, you must design with the constraints of the material and making process in mind.

+Let's give our tower a facade!

In the last exercise, we designed our building floors as curved ellipses, which was relatively easy to do with one component in Grasshopper. In reality, though, most building materials come in flat sheets, which are easier to manufacture and cheaper to transport. Considering the scale of the building, describing the facade as a series of flat panels that follow the outline of the ellipses would probably achieve a very similar effect, though at a much lower cost. In architectural design, the process of refining a model's geometry so that it takes into account the constraints of the material and process used to build it is called rationalization. In this exercise, we will rationalize our simple curved facade by describing it as a series of flat rectangular panels.

This exercise will pick up from the last one. If you don't have that model handy you can download it here:

+Step 1: Design concept and strategy

Our goal in this exercise is to create a set of rectangular, flat panels as individual surfaces that approximate the elliptical floor plates as much as possible. To define each rectangular surface, I need four points that define its corners. To make sure the panels follow the ellipse I can place these points on the floor profile curves at regular intervals. This will give me a set of points defining the lower edge of each panel. I can then move the set of points up to define the upper set of points. I then need to create a computational strategy for going through these sets of points, choosing the right set of 4 points each time to create each panel.

+Step 2: Make some points

To create the points, we will use the Divide Curve component, which we already saw in the first exercise. Let's create a new Divide Curve component and connect its (C) input to the Rotate component's (G) output which is storing all the curves representing the floor outlines. By default, this will create 10 points evenly distributed on each floor curve, but we can control the number of points created by connecting a number into the Divide Curve component's (N) input.

Let's say, however, that we don't know how many panels each floor needs. Instead, we may want to specify the maximum size of any panel. We can build this into our definition by first using a Curve Length component to find the length of each curve, and then dividing that length by the maximum width we want for the panels (I'll use 10'-0"). This division will give us the number of panels (and thus the number of curve divisions) we need to make sure our panel ends up the proper width.

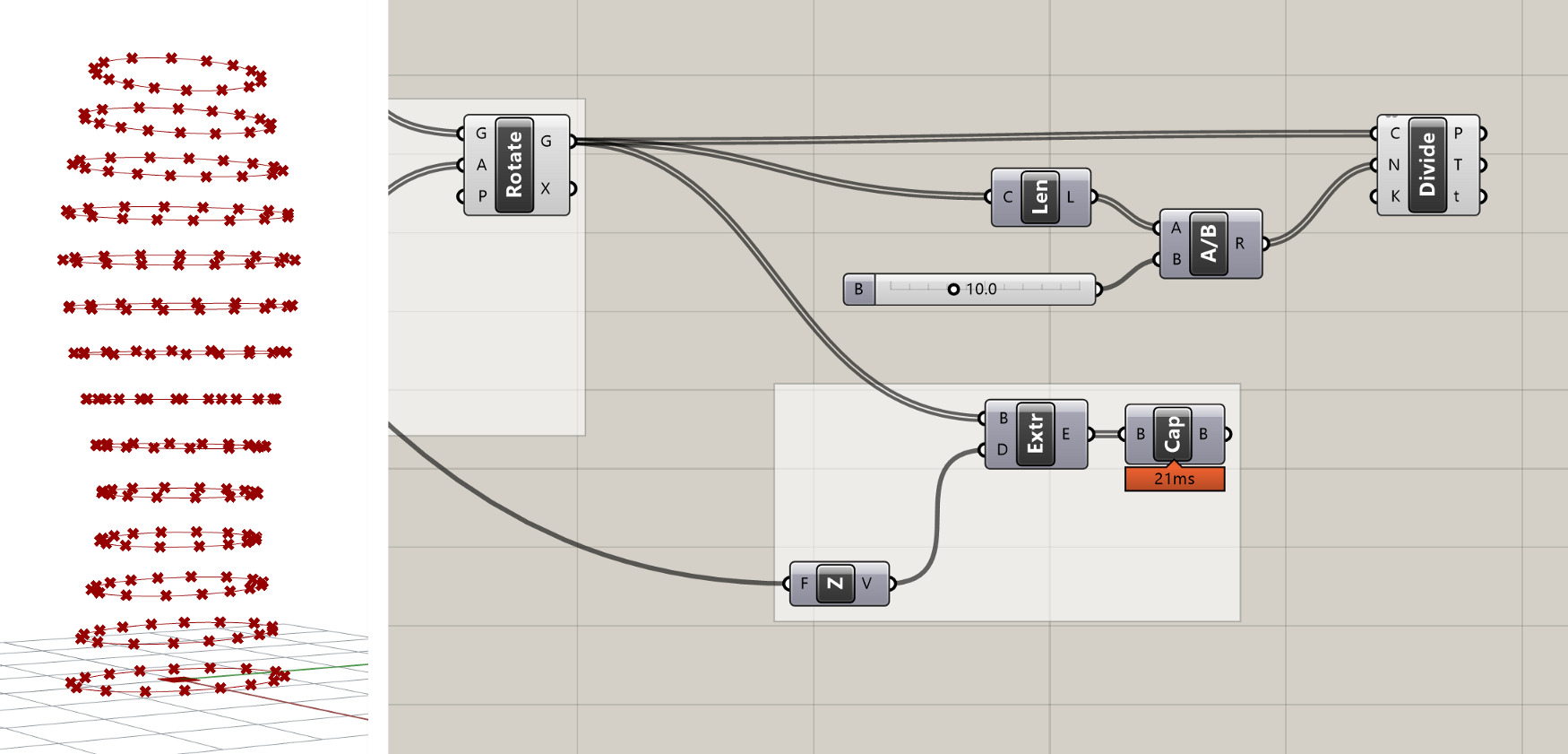
Because the length of the curves will not necessarily be evenly divisible by the target width of the panel, the division will most likely produce a decimal number. If you plug this number directly into the 'N' input of the Divide Curve component, the component will automatically round to the nearest integer. However, depending on whether we round up or down, the final panel width may end up being slightly smaller or slightly larger than the target. To ensure that our panels are always no wider than 10'-0", we need to force the division to round up. We can do this with the Round component, which takes a decimal number and gives us three options for how to round it: Nearest, Floor (force round down), and Ceiling (force round up).

Comparing the three outputs of the Round component

If you hover over the 'P' output of the Divide Curve component, you will see that the data is organized as a DataTree. Instead of listing the actual data, the tooltip now lists the path and number of items in each branch of the DataTree. In this case, we have 14 branches in the DataTree (one for each floor of our building), with 16 points in each branch representing the 16 points generated by dividing each curve.

Tooltip showing the structure of the DataTree produced by the Divide Curve component

The DataTree was created automatically by Grasshopper because we supplied a List of Curves to the Divide Curve component which itself produces a List of points for each Curve. The Divide Curve component runs once for each Curve and puts the resulting points on a separate branch of the DataTree. Although DataTrees can be confusing at first, they are actually quite helpful for organizing data in proper hierarchies based on how the model is built. Without DataTrees, we would be stuck with one long list of points after our division, which would make the rest of this exercise much more challenging.

+NOTE

It would be challenging but not impossible. In fact, before DataTrees were implemented in Grasshopper there were many workarounds for doing this using clever data manipulations. As an extra challenge, try flattening the set of points coming out of the Divide Curve component, and see if you can work through the rest of this exercise and still generate the proper final output.

The points generated by the Divide Curve component will define the lower two corner points of each panel. To define the upper corner points we can use a Move component to create another version of the points moved up to the top of each floor. We can reuse the Unit Z component we created previously for the extrusion to specify the translation vector of the move.

+Step 3: Create the panels

Now that we have the points, we need to define the actual panel geometries based on those points. To create a Surface object from four corner points, we can use the 4Point Surface component. This component has four individual inputs where we can connect the four corner points to create a Surface. We can create all the panels of our building at once by supplying a list of points to each input, but the lists have to be aligned so that the right points are available for each panel as it's being created.

Currently, we have two Lists of points defining the upper and lower corners of each panel. If we iterate through each list simultaneously, this will give us the leading two points of each panel. To define the other two points, we can actually reuse the same Lists of points, since the trailing points of one panel become the leading points of the next.

However, to make sure the right points align for each panel, we first need to shift the Lists by one spot, so that the first panel actually gets the second point from each new List. To shift the Lists we can use the Shift List component, which will shift the items in a List to the left by the number of spots indicated in its Shift (S) input. Let's create two new Shift List components and connect their (L) inputs to the outputs of the Divide Curve and Move components that are storing our point data.

The Shift List component's Shift (S) input is set to 1 by default, which will shift the List one spot to the left, meaning the second item will now become the first. Since this is exactly what we want, we can leave the default value. Once the definition is complete, feel free to experiment with this input to see how the shift factor affects the way the panels are created. You can also try inputting negative values to shift the List in the other direction.

Now that we have our four sets of points for the four corner points of each panel, we can connect them to the 4Point Surface component. This component expects you to enter the corner points in counter-clockwise order. Based on the diagram we can connect the original points to the (A) input, the shifted version of the original points to the (B) input, the shifted version of the moved points to the (C) input, and the moved points to the (D) input.

When everything is properly connected you should see the flat panel geometries appear properly in the model. If you don't see the panels or they appear twisted you may have input them in the wrong order. Make sure your solution matches the image below before proceeding.

Panel geometries created by the 4Point Surface component

You've probably noticed that the Shift List components also have a third input called Wrap (W) which specifies whether the elements moved off the end of the list should wrap around and be placed at the other end. In our case, we will leave this at the default 'True' because we want the first points in each list to wrap around to the end of the shifted Lists so they can be used to create the last panel on each floor. Try to set these to 'False' and you will see that the last panel on each floor will not be created correctly.

+Step 4: Create openings

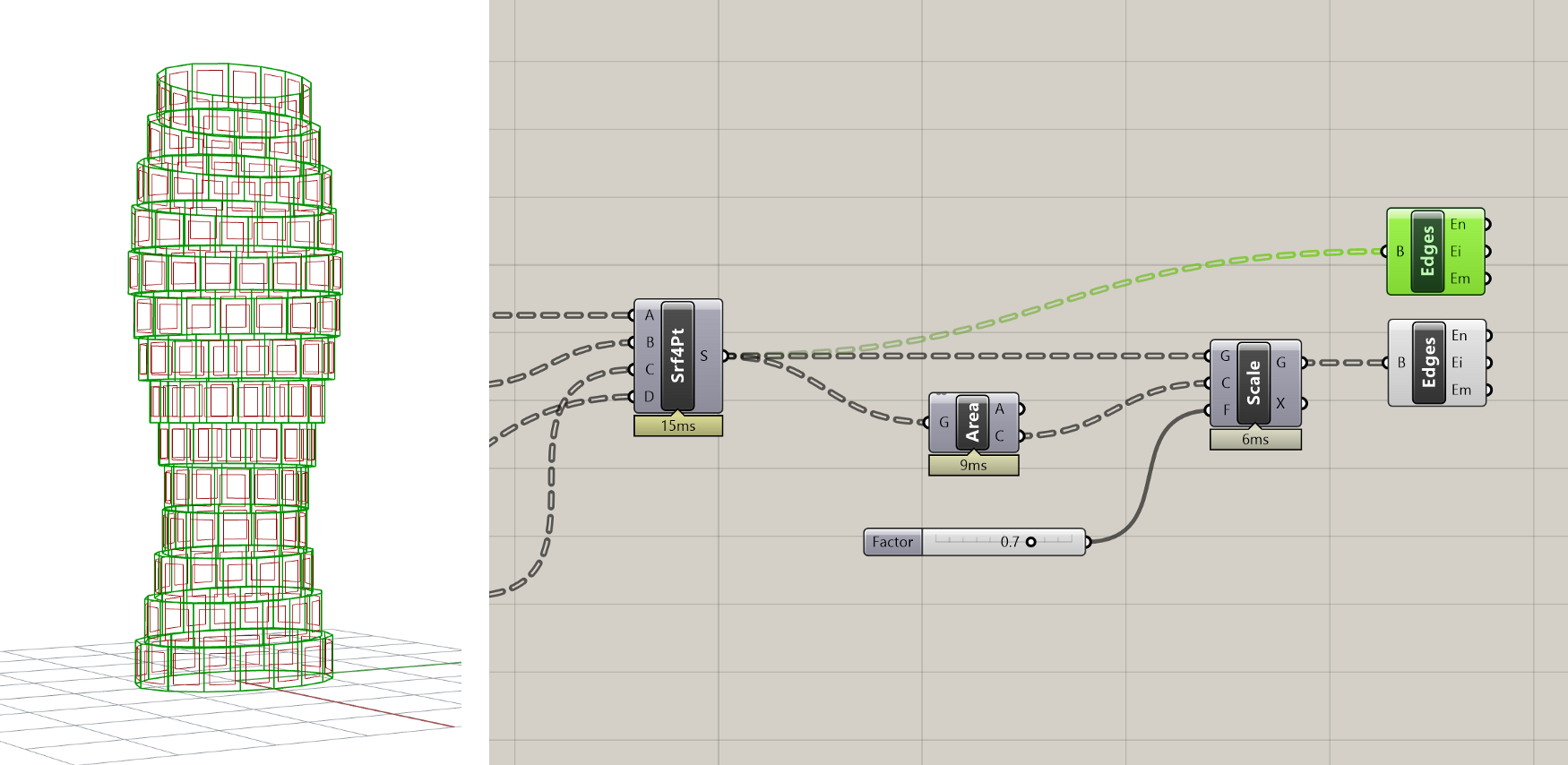
Now that the basic panels are created, let's add some detail by creating an opening in each panel. Our strategy for creating the openings will be to first scale each surface to make a smaller surface, then extract the edges of both surfaces and use the edges to construct a single surface with a hole in it.

To scale the surfaces, we will use the Scale component, which scales an object based on a center point and scale factor. Place a new Scale component on the canvas and connect its (G) input to the panel surfaces stored in the (S) output of the 4Point Surface component. This will create a half-size version of the tower since the default scale factor is 0.5 and the default center point for scaling each panel is the model origin.

To scale each panel relative to its own center point, we need to first generate a set of points at the panel centers and then pass these points to the Scale component. A good way to get the center point of a flat object such as a surface or closed curve is to use the Area component, which will compute the area of the object as well as its centroid.

Let's create a new Area component and connect it to the panel Surfaces. You should see a point object appear in the model at the center of each panel. Now let's pass this List of points to the (C) input of the Scale component. Each surface should now be scaled relative to its own center, with a smaller surface sitting on top of the original one. Since we're using the same Surfaces we're scaling to generate the center points, we can be sure that the number of Surfaces and points will match and that the right point will be used to scale each Surface. To finish things off, let's make a new Number Slider component and connect it to the (F) input of the Scale component so we can control the scale factor (and thus the size of the openings).

+Step 5: Rebuilding the panels

Once we've defined the scaled Surfaces, we can extract the edges of both sets of Surfaces so we can use them to define the final panel geometry.

To extract the edges of a Surface or Polysurface object, we can use the Brep Edges component. This component produces both the naked edges (En) which are on the boundary of a Surface or Polysurface object, as well as the interior edges (Ei) where two Surfaces are joined within a Polysurface. Since our panels are represented by singles Surfaces, we are only interested in the naked edges which form the Surface's outer boundaries. Let's create two new Brep Edges components and connect them to both the original and scaled Surfaces.

Next, let's combine the two sets of edge curves into a single data stream using the Merge component. This component will combine multiple data sets into one based on the structure of the data coming in:

• Merging single elements will create a List with the elements ordered based on the order they were input into the component
• Merging multiple Lists will create one List with all elements ordered based on the order they were input into the component
• Merging DataTrees will create a new DataTree with elements combined in branches with the same path. Remember that a List is just a DataTree with a single branch, so if you combine a DataTree with a List it will put the List's data on the default {0;0} branch of the new DataTree.

The Merge component supports an unlimited number of input streams and has a zoomable UI which you can use to add and remove inputs. A new input will be automatically added every time you plug one in, which also speeds up the workflow. Let's create a new Merge component on the canvas and connect to it both sets of edge curves.

Since our edge curve data is in DataTree format, it is very important that both DataTrees share the exact same structure, so that all the curves from one panel end up on the same branch. Some components may add extra levels of hierarchy to data as it's passed through them, which can mess up the matching during Merge. To ensure that both inputs have the simplest possible DataTree representation, we can right-click on both inputs and select the 'Simplify' filter.

Results of Merge operation showing DataTree with branches organized according to building floor and panel, with 8 curves on each branch defining the boundary edges of each panel.

Once we have all the panel boundary curves in individual branches of a single DataTree, we can pass them into a Boundary Surfaces component to construct the final panel geometry. This component is similar to Rhino's PlanarSrf command. It takes in any number of co-planar flat curves and creates a single surface trimmed to the edges of all the curves. For curves completely contained within curves such as our example, it trims a hole within the larger surface.

Once we have all the panel geometries, the last step is to join all the panels on each floor together to create a single Polysurface for each floor. We can do this using the Brep Join component, which will take any number of Surfaces or Polysurfaces and combine them into a single Polysurface if they share common edges.

Before we can join the panels together, we need to make sure that all the Surface geometries we want to join are located on the same branch. Remember that components are designed to take a certain number of items in each input. If a component's input is designed to take one item and you pass into it a List or DataTree, the component will run once for each item. The Brep Join component is designed to take a List of Surfaces and join them all together. When we pass a DataTree of Surfaces, the component will run once for each branch, attempting to join all the surfaces contained in each.

Currently, each of our panel Surfaces are on separate branches, so nothing will happen if we try to join them. To get all the panels on one floor to be on the same branch, we need to remove the last level of hierarchy in the DataTree (based on how we constructed the model, the first level of hierarchy represents the floors and the second level represents the panels). An easy way to remove the last branch level of a DataTree is by using the Trim Tree component, which will merge outer branches of a DataTree based on the Depth (D) provided. The default depth is set to 1, which trims the most outer branch.

As an alternative, you can use the Path Mapper component with the 'Trim' preset. This will put all the panel geometries on the same floor on the same branch, going back to the DataTree structure we had originally (before the Edges components added a level of hierarchy). Now when we input the trimmed DataTree into the Join component, all the panel geometries will be joined into one Polysurface per floor.

+Step 6: Create floors

Now that each floor's facade geometry is defined, the last step is to rebuild the floor and ceiling of each floor so we can join it with each floor's facade and end up with one joined Polysurface for each floor. In the previous exercise, we used the Cap Holes component to automatically close planar openings in the extrusion geometry. This will also work here, but since our facade openings are also planar holes, the Cap Holes component will fill those as well.

Instead of capping the holes automatically, let's manually build the new floor and ceiling geometries based on the same points that define the corners of the facade panels. First, we will create the outline of the floors by inputting the points created by the Divide Curve component into a Polyline component, which will connect the points on each floor into a single Polyline. Make sure to set the Polyline component's Closed (C) input to True so that a closed Polyline is created for each floor. Otherwise, you will be missing the final segment connecting the last point in each list back to the first.

A nice visual way to control Booleans in your definition is by using the Boolean Toggle Input component, which will create a new Boolean variable and allow you to toggle between True/False values by double-clicking on the label.

Once we have the boundary curve for each floor defined, we can use the Boundary Surfaces component to create a planar surface for each floor, and the Move component to move each floor up to form the ceilings. For the Move component's translation vector we can reuse the same vector we used to create the top set of corner points for the panels.

+Step 7: Join it all together

Now that we have the facade, floor, and ceiling defined for each level of the building, we can use the Merge and Brep Join components one more time to combine the data into one DataTree and merge all the geometries into one Polysurface per level. In order for this to work, we have to be sure that all the DataTrees going into the Merge component share the same structure—a branch for each level of the building with each branch containing all the geometry from that level. To make sure all the branches line up, you can apply the 'Simplify' filter to each input of the Merge component.

If everything worked right, we should end up with one Polysurface for each level of the building. Since we used the same set of points to build all the Surfaces, we can be sure that everything will line up correctly and join together perfectly. Such is the beauty of computational design—it may take some time to build everything right, but once it's built you can be sure that everything will function the way it's supposed to. If you did get lost along the way or something didn't turn out the way you expected, you can download a finished version of the demo here:

+CHALLENGE 3: Cutting corners

If you figured out the last challenge by using a Rectangle component to replace the elliptical floors with rectangular ones, you may see an issue applying the paneling in this exercise. Since each rectangle is a single Curve, depending on how they get divided you could see that some of the corners get cut or chamfered. Can you think of a way to solve this problem and force the facade panels to always end at the corners?

+Conclusion

In this exercise, we rationalized the tower geometry by generating a set of flat panel surfaces to approximate the curved shape of the tower. We also added an opening to each panel whose size can be controlled by a parameter. Spend some time experimenting with the model to see what kinds of variations and panel geometries you can create.